Tag: lunar maximum

Understanding Lunar Maxima: Ancient Insights Explained

Stone Age astronomy focused on celestial time cycles and natural units, allowing astronomers to develop intricate cosmic meanings. As civilizations advanced, attention shifted to space and scientific models, diminishing the intimate connection to time. Notably, the development of megalithic measurements reflected their unique perception of time, emphasizing a geometric understanding of their environment.

figure 1: The north-east quadrant of the horizon from the megalithic sites of Carnac. At that latitude, alignments to the solar and lunar extremes followed a simple geometry of multiple squares, repeated in all four quadrants, the observer in this quadrant being placed bottom left.

It was most fortunate for the stone age astronomer that the time periods surrounding the earth could be counted in whole numbers of natural units such as the solar day, the lunar month, and the lunar orbit. Over longer periods, whole number fractions would become whole, revealing special cosmic numbers, then symbolic of the cosmic time periods associated with planets, eclipses and other coincidences, so that a large matrix of relationships gave the Stone Age a world of meanings in the sky based upon time and number.

Continue reading “Understanding Lunar Maxima: Ancient Insights Explained”

Easter Aquhorthies

Easter Aquhorthies (i.e. apocathery) has eleven stones in a circle and in between the two south-to-south-west stones is a large (bridging) recumbent stone, more commonly found in Scottish circles  and associated (by Alexander Thom) to lunar observatories because, in Scotland at lunar maximum standstill, the moon can rest upon or be hidden by a raised horizon.

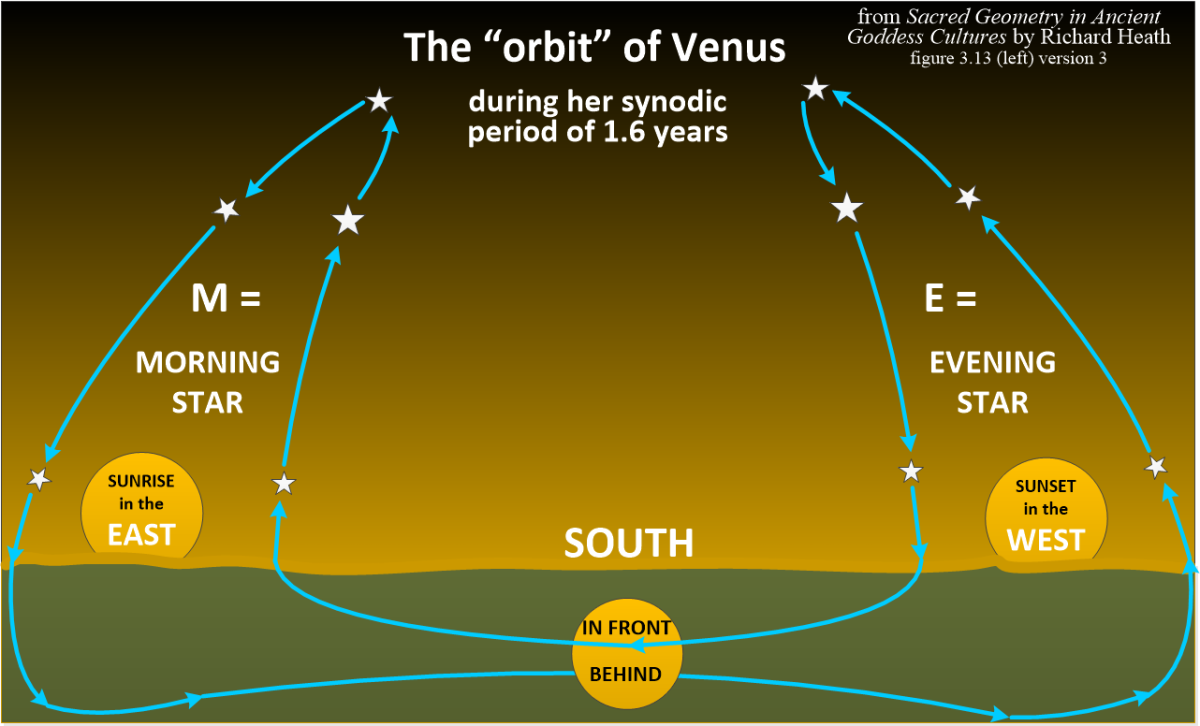
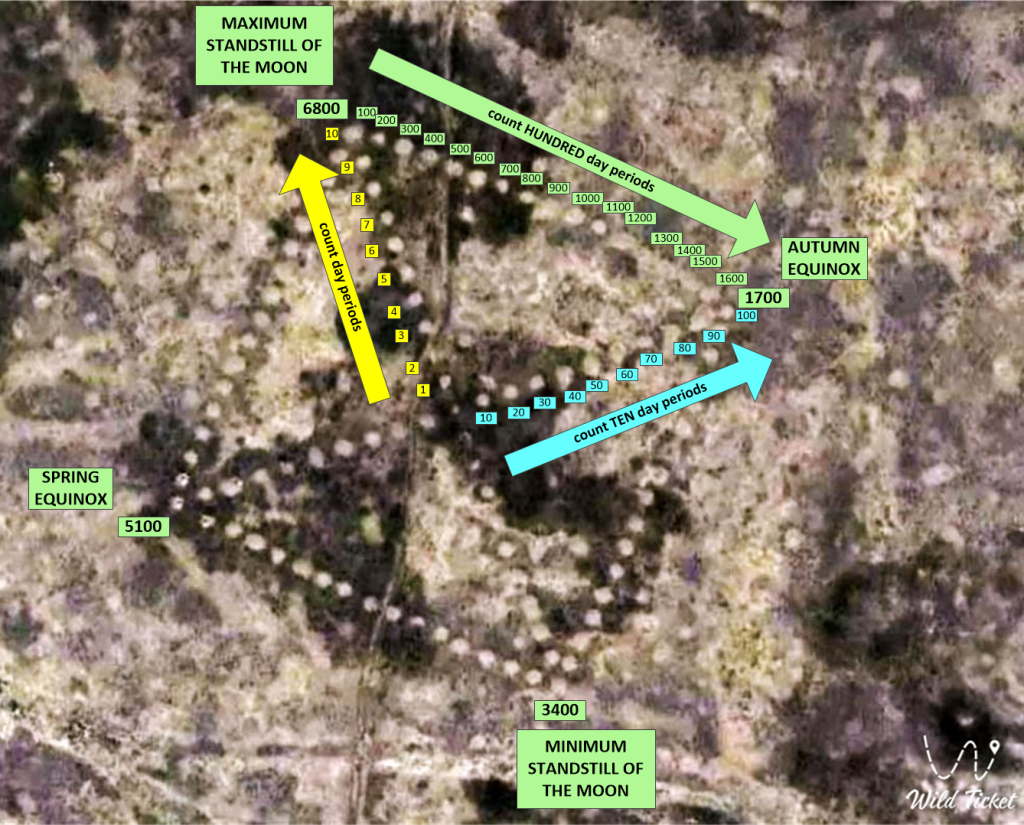
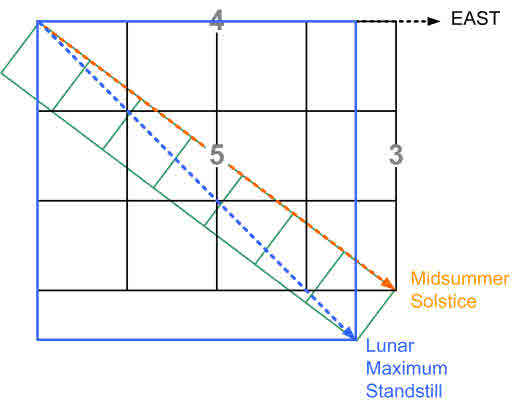
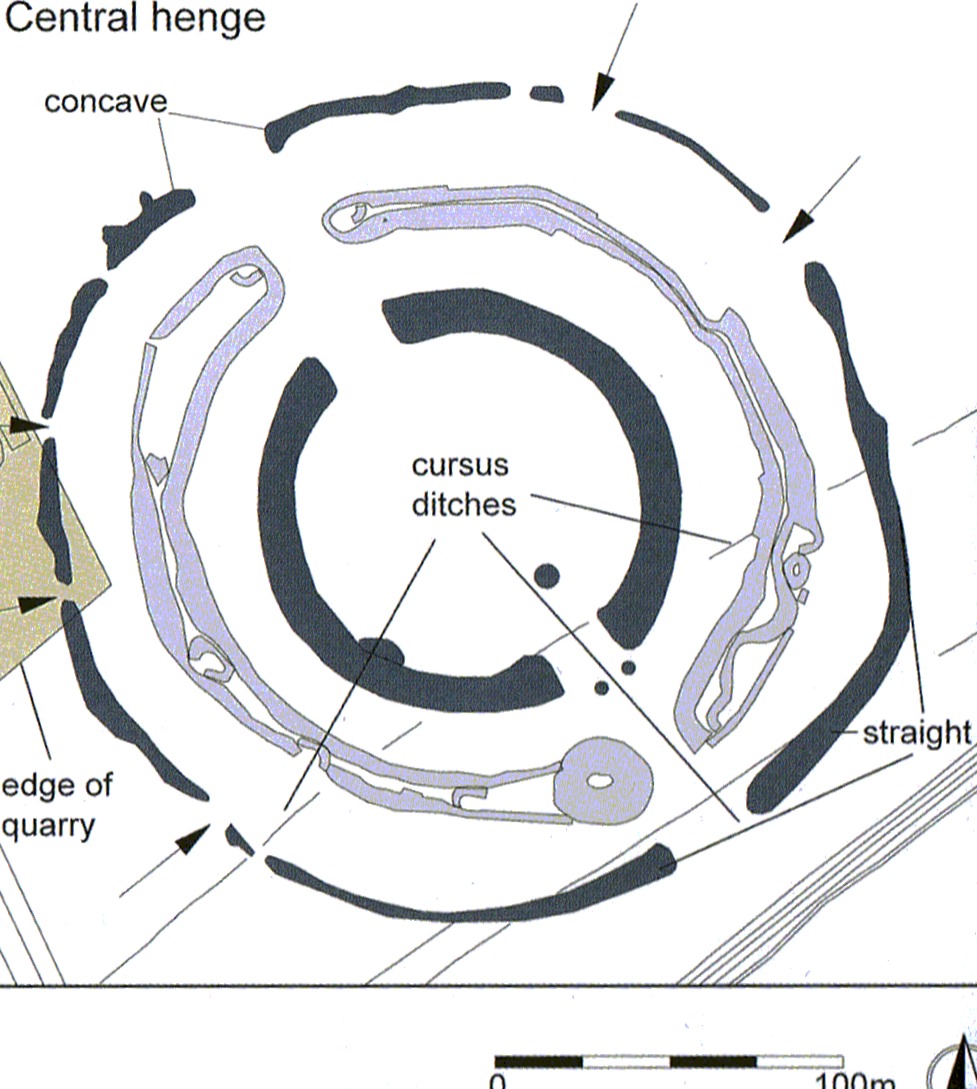
Picture by krautrock, a member of megalithic.co.uk in June 2010.

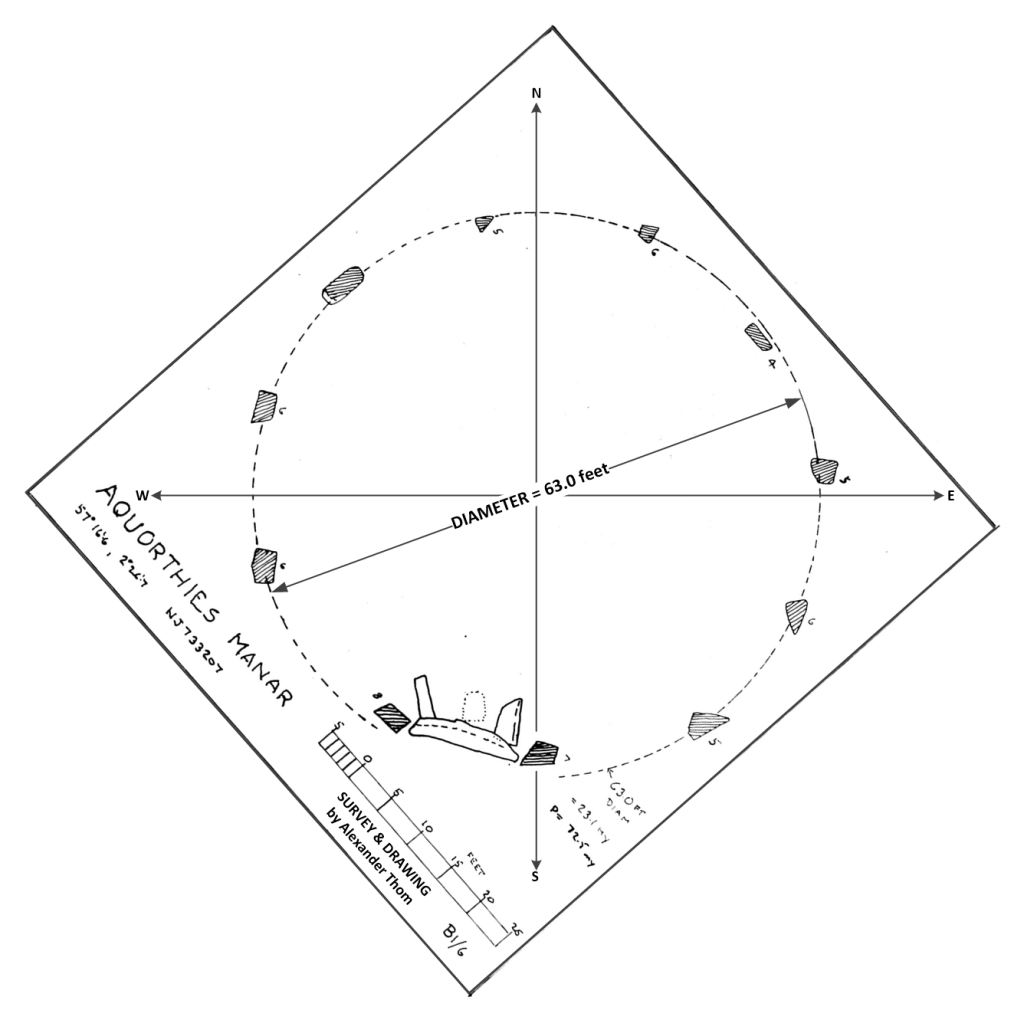
Figure 1 Alexander Thom’s site plan, with cardinal directions and highlighting the diameter .

It is tempting to assume geometry within stone circles and this one invites that by having eleven regularly placed stones,. However, 11 is rarely found in regular geometries or stone circles.

Continue reading “Easter Aquhorthies”

The Geocentric Orbit of Venus

It is helpful to visually complete the movement of Venus over her synodic period (of 1.6 years) seen by an observer on the Earth.

figure 3.13 (left) of Sacred Goddess in Ancient Goddess Cultures
version 3 (c) 2024 Richard Heath

In the heliocentric world view all planets orbit the sun, yet we view them from the Earth and so, until the 16th century astronomy had a different world view where the planets either orbited the sun (in the inner solar system) which like the outer planets orbited the earth, this view called geocentric. The discovery of gravity confirmed the heliocentric view but the geocentric view is still that seen from the Earth.

The geocentric was then assumed to be wholly superseded, but there are many aspects of it that appear to have given our ancestors their various religious views and, I believe, the megalithic monuments express most clearly a form of astronomy based upon numbers rather than on laws, numbers embedded in the structure of Time seen from the Earth, and hence showing the geocentric view had more to it than the medieval view discarded by modern science.

Venus was once considered one part of the triple goddess and the picture above shows her complete circuit both in the heavens and in front of and behind the sun. The shape of this forms two horns, firstly in the West at evening after sunset. Then she rushes in front of the sun to reemerge in the East to form a symmetrical other horn after which she travels behind the sun to eventually re-emerge in the West in a circuit lasting 1.6 years of 365 days, more precisely in 583.92 days – her synodic period.

Continue reading “The Geocentric Orbit of Venus”

Utility of the Ushtogai Square to count the Nodal Period

Using Google Earth, a large landform was found in Kazakhstan (Dmitriy Dey, 2007); a square 940 feet across with diagonals, made of evenly spaced mounds. We will demonstrate how the square could have counted the lunar nodal period of 6800 days (18.617 solar years)

 images courtesy of Wild Ticket

Counting the Lunar Nodal Period

One can see the side length of the square contains seventeen (17) mounds, with 16 even distances between the mounds. Were one to count each side as 17 mounds, then four times 17 gives 68 which reminds us of the 6800 days in the moon’s nodal period of 18.617 years. If 17 can be multiplied by 100, then one could count the nodal period in days, and to do this one notices that the diagonals have one central space, around which each of four arms are 10 mounds long.

The Ushtogai Square from above, north to the top.

Continue reading “Utility of the Ushtogai Square to count the Nodal Period”

Angkor Wat: Observatory of the Moon and Sun

above: Front side of the main complex by Kheng Vungvuthy for Wikipedia

In her book on Angkor Wat, the Cambodian Hindu-style temple complex, Eleanor Mannikka found an architectural unit in use, of 10/7 feet, a cubit of 20/21 feet (itself an outlier of the Roman module of 24/25 feet, at 125/126 of the 0.96 root Roman foot).

She began to find counted lengths of this unit, as symbols of the astronomical periods (such as 27 29 33) and of the great Yuga time periods proposed within Vedic mythology. Hence Mannikka’s title of Angkor Wat: Time, Space, and Kingship (1996). Whilst the temple was built by the Khymer’s greatest king, their foundation myth indicates the kingly line was adopted by a matriarchal goddess tradition.

Numerically Symbolic Monuments

Continue reading “Angkor Wat: Observatory of the Moon and Sun”

Gavrinis 1: Its dimensions and geometrical framework

This article first appeared in my Matrix of Creation website in 2012 which was attacked, though an image had been made. Some of this material appeared in my Lords of Time book.

photo For Wikipedia by Mirabella.

Gavrinis and Tables des Marchands are very similar monuments, both in the orientation of their passageways and their identical latitude. Gavrinis is about 3900 metres east of Tables des Marchands but, unlike the latter, has a Breton name based upon the root GVR (gower). Both passageways directly express the difference between the winter solstice sunrise and the lunar maximum moonrise to the South, by designing the passages to allow these luminaries to enter at the exact day of the winter solstice or the most southerly moonrise over many lunar orbits, during the moon’s maximum standstill. Thus both the monuments allow the maximum moon along their passageway whilst the winter solstice sunrise can only glance into their end chambers.

From Howard Crowhurst’s work on multiple squares, we know that this difference in angle is that between a 3-4-5 triangle and the diagonal of a square which is achieved directly by the diagonal of a seven square rectangle.

Figure 1 The essence of difference between the winter solstice sunrise (as diagonal of 4 by 3 rectangle) and southerly maximum moonrise (as diagonal of a single square), on the horizon, is captured in the diagonal of a seven squares rectangle.
Continue reading “Gavrinis 1: Its dimensions and geometrical framework”